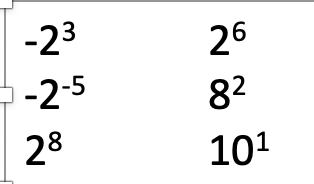In mathematics, we always come across exponents. So, what are exponents and its features?
The Definition
Exponents on numbers are simply how many times it multiplies itself. For example, 43 = 64 because 4 x 4 x 4 = 64. Also, we use “Four to the power of three”, or “Four to the third power” in speaking. That’s way more straightforward than 4 x 4 x 4, right?
Even though it is that simple, there are many usages of exponentiation, from solving an equation to making a complex machine.
Negative Exponents
But, how about negative exponents? How can we calculate that? Well, just flip the number into a relevant positive number, and divide one by it. For instance, for 2-3, it is 0.125. So, try to think of the process by the example and the text above. If you still don’t understand, read the answer below and make your question!
Also, for exponents of negative numbers, we need to use the negative number if the exponent is an odd number, and we need to use the positive number if not. For instance, (-3)2 is 9, while (-3)3 is -27. Therefore, the square root of 25 can be -5! But, remember to use a bracket or the value is different. This is also suitable in any exponents with a calculated value, like (ab)2.
How about the first and zeroth power?
There is probably something missing in this article, and that’s the first and zeroth power. In fact, it’s elementary, with the zeroth power always is 1, and the first power is the number itself if the number is positive.
You may be curious why the zeroth power is 1 instead of 0, but here’s the explanation for you, with a formula worth learning:
So, this article shows what are exponents, how to use them, and common questions about that.
References, Credits and Links
- (n.d.). Squares and Square Roots – Math is Fun. Retrieved November 6, 2020, from https://www.mathsisfun.com/square-root.html
- (n.d.). Exponents – Math is Fun. Retrieved November 6, 2020, from https://www.mathsisfun.com/exponent.html