What Is a Barycenter?

Think of the scene where the Moon orbits the Earth. Do you view Earth as a fixed point, or do you think it’s wobbling? If you think the former scenario is true, you would be wrong. Today, we’ll explain what a barycenter is and how this causes the Earth to wobble.

The barycenter is the center of mass of an N-body system, where every object in that system orbits. Take the two-body problem as an example. There are two gravitationally interacting bodies traveling at a relative speed without anything else perturbing them. However, not only does the more massive object exert a force on the small body, the less massive object also perturbs the larger body. Therefore, rather than saying that the smaller body (the secondary object) orbits the larger one (the primary object), it’s better to say that they orbit each other.

But where are they orbiting? They are going around their center of mass, or barycenter. For a two-body system, it’s very simple. We just put the two bodies opposite each other relative to the barycenter. But for an N-body system where N > 2, it’s more complicated, as the positions of all bodies must be taken into account when computing its location.

What affects the location of the barycenter? The two factors are the relative masses of the objects and the distances between the objects. The larger the secondary-to-primary ratio, the closer the two bodies are in terms of mass, and the further apart the barycenter is from the primary object. Also, the farther the bodies are from each other, the farther the barycenter is, even though the ratio between the distances from the primary to the barycenter and the distances from the primary to the secondary remain constant.

Specifically, the barycenter is located at

where d is the distance, p is the mass of the primary, and s is the mass of the secondary.

Every N-body system has a barycenter, but we’re listing the more prominent or notable examples of them in this article. For example, even though Jupiter is 1000 times less massive than the Sun, the barycenter between the Sun and Jupiter lies outside the surface of the Sun! That’s because of the large distance between the two objects, which is 5.2 astronomical units. Other planets perturb the Sun’s trajectory around the barycenter as well, so it appears to wobble in complicated paths with respect to the barycenter.

The Earth-Moon system is another interesting example. The Moon is only about 1.2% as massive as Earth, but its mass still causes our planet to wobble. In fact, the Earth-Moon barycenter, where the Earth and the Moon both orbit, lies about 1600 kilometers below the surface of the Earth. Given that the Earth’s radius is 6371 kilometers, the barycenter is relatively high up our planet.

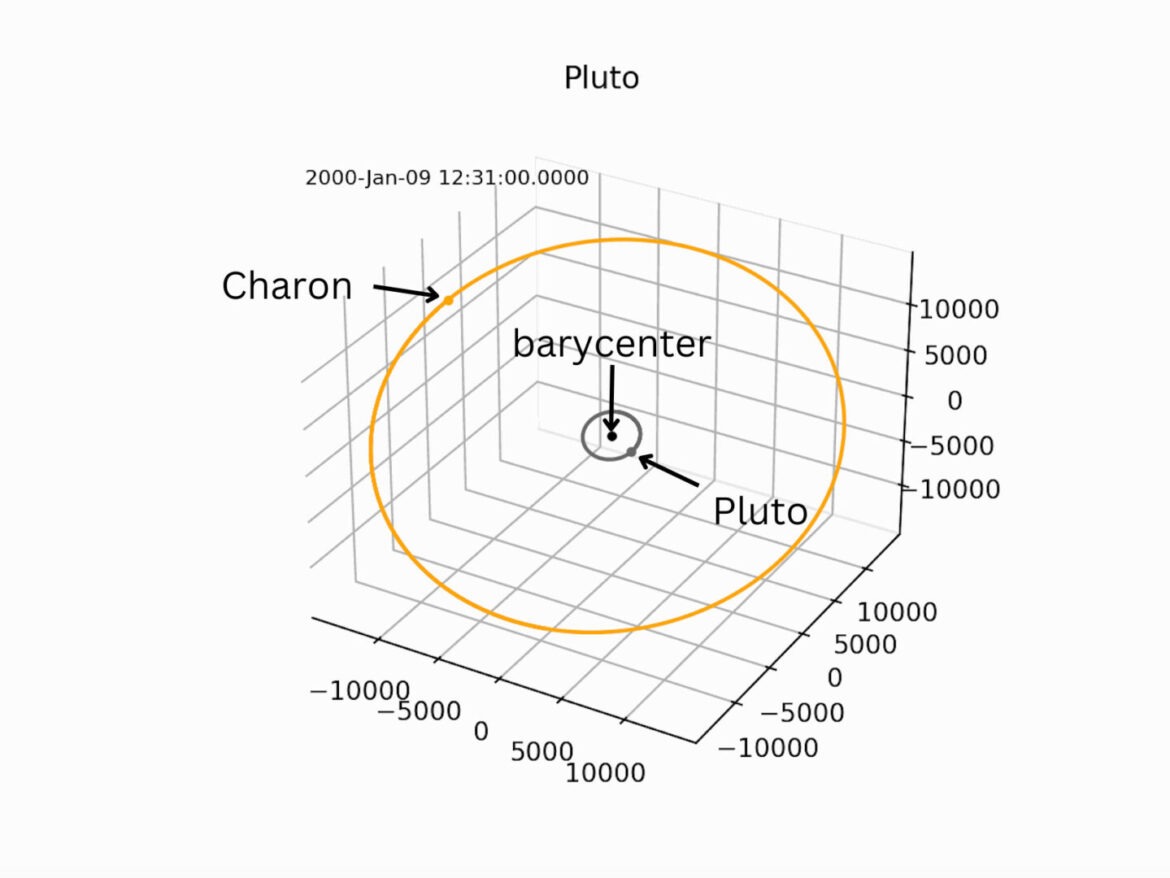
An even more extreme example can be seen on the dwarf planet Pluto. Pluto has five moons, of which four are asteroids, but one is a planetary-sized body. In fact, it is about half the size of Pluto, and only about eight times less massive. Its barycenter lies outside the surface of Pluto, and so Pluto is orbiting a point outside its body. This is similar to the case of the Sun, though due to the small mass of the remaining moons, the barycenter always remains outside Pluto.

Moreover, the phenomenon of barycenters also helps scientists spot exoplanets. If a planet is in orbit around a star, the star also wobbles a little bit because of the planet’s mass. This creates slight redshifts and blueshifts in the data, where the star’s spectrum moves toward the low-energy or high-energy directions. This shift is detectable by telescopes and tells how far the star wobbles. If the variation is periodic, it might indicate the existence of an exoplanet. This is called the radial velocity method, which is one of the primary ways astronomers find planets outside our Solar System.

In this article, we have introduced that a barycenter is the center of mass in a system where all bodies there orbit. Through this principle, the moons can significantly change the planets’ positions. Thus, when predicting astronomical events or dealing with close encounters, you also need to account for the satellites. If you would like us to include more content, please leave your suggestions in the comment section below.