Your computer is probably dealing with billions of bits a single second using instructions given by various program developers, but how does it do so at the most fundamental level? Well, computers use small logic gates that create powerful instructions when chained together at the right way. Let’s find out about them in this article.
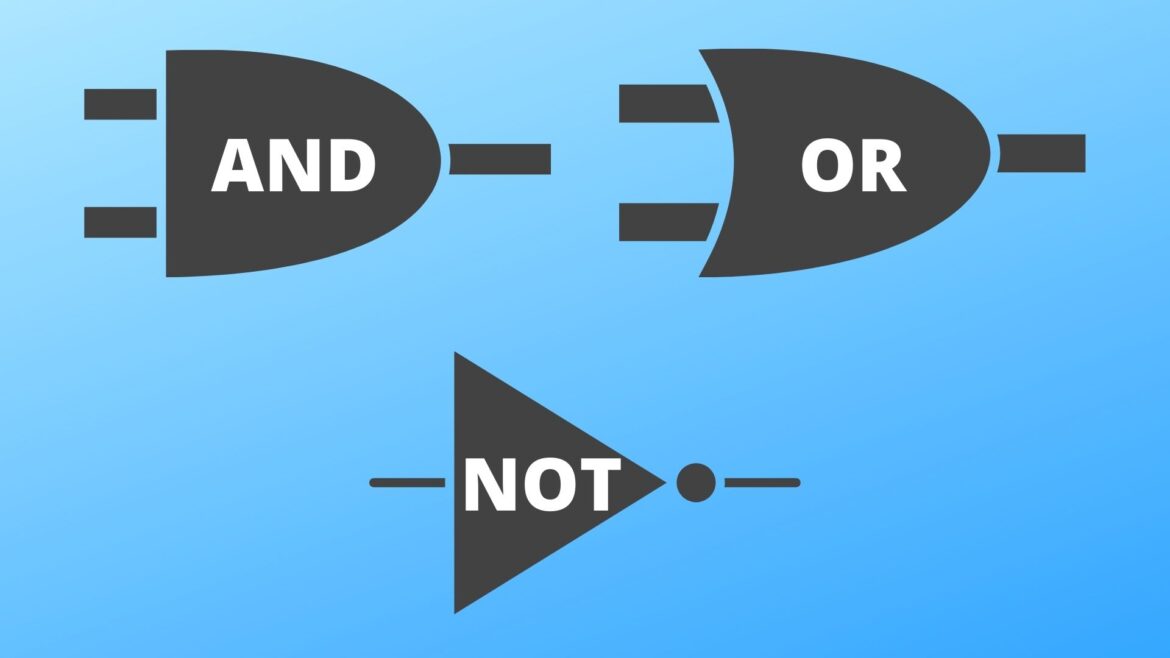
The Three Logic Gates
There are three important logic gates for computers to manipulate bits. Here are the names of them:
- AND
- OR
- NOT
The AND gate only returns a value of 1 if both inputs are 1, and the OR gate returns a value of 1 if either or both of the inputs are 1. The NOT gate is different from the other two gates as it only accepts one bit as input, and it flips the bit. That means if the input is 0, the output will be 1, and if the input is 1, the gate will return a value of 0. Here is the table for the outputs corresponding to each gate and each set of input values.
| GATE | INPUT 1 | INPUT 2 | OUTPUT |
| AND | 0 | 0 | 0 |
| 0 | 1 | 0 | |
| 1 | 0 | 0 | |
| 1 | 1 | 1 | |
| OR | 0 | 0 | 0 |
| 0 | 1 | 1 | |
| 1 | 0 | 1 | |
| 1 | 1 | 1 | |
| NOT | 1 | NULL | 0 |
| 0 | NULL | 1 |
What About Other Logic Gates?
You might have heard of logic gates other than the AND, OR, and NOT gates, like the XOR, NOR, and NAND gates. However, they can be chained from the three fundamental logic gates mentioned above.
A NAND gate is easy to construct because it only requires an AND gate and a NOT gate chained together. Likewise, a NOR gate only needs an OR and NOT gate to be made. The XOR gate is more complicated to build, but it can be built from one AND gate, one OR gate, and a NAND gate.
But what are these logic gates exactly? A NAND gate is the reverse of an AND gate, and a NOR gate is the reverse of the OR gate, as mentioned in the preceding paragraph. A XOR gate is also easy to understand, as it returns a value of 1 when the two inputs are not the same, and returns 0 in other cases. Just in case you are still confused with them, here is the table of outputs associated with the different inputs and gates.
| GATE | INPUT 1 | INPUT 2 | OUTPUT |
| NAND | 0 | 0 | 1 |
| 0 | 1 | 1 | |
| 1 | 0 | 1 | |
| 1 | 1 | 0 | |
| NOR | 0 | 0 | 1 |
| 0 | 1 | 0 | |
| 1 | 0 | 0 | |
| 1 | 1 | 0 | |
| XOR | 0 | 0 | 0 |
| 0 | 1 | 1 | |
| 1 | 0 | 1 | |
| 1 | 1 | 0 |
Building the Adder
After learning about the basic logic gates, you can make instructions out of these straightforward gates. One of the structures you will learn about when encountering logic gates is the adder, which will be explained in the following parts of the article.
To make an adder, we first have to make a half adder. It’s an adder that is able to add two one-bit inputs. This gate is made of a XOR gate and an AND gate, with the XOR gate handling the unit digit and the AND gate handling the twos digit. Here is a table for the outputs produced when it encounters two bits as input:
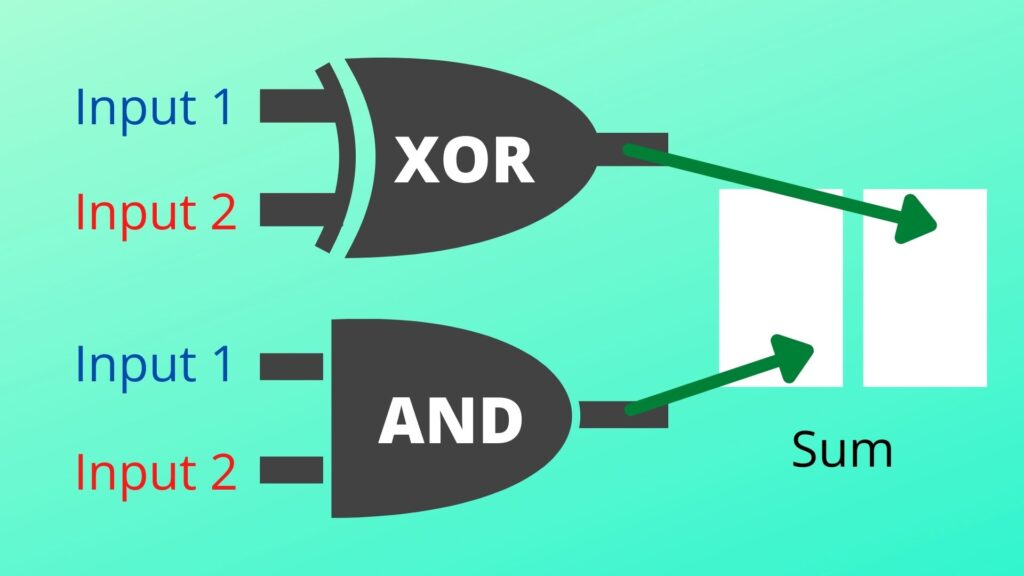
Image created using Canva
| GATE | INPUT 1 | INPUT 2 | OUTPUT |
| Half adder (XOR + AND) | 0 | 0 | 00 |
| 0 | 1 | 01 | |
| 1 | 0 | 01 | |
| 1 | 1 | 10 |
After discovering that the half adder can add two one-bit numbers, it is possible to construct a full adder supporting carry operations by chaining the half adders together. Basically, the two half-adders are connected by adding an OR gate between the two AND gates so that the carry operation can be done. The full adder adds three binary digits into a two-bit result. Two of the bits are bits from the numbers to be added, while the other bit is whether the carry operation should be done. By chaining full adders together, we can add numbers as large as you’d like.

Image creates using Canva
Conclusion
Besides the adder, we can build much more complicated instructions on logic gates, which we can use to build algorithms. Remember that when you use your computer, you are harnessing the power of small, easy-to-understand logic gates chained together to make complicated algorithms. If you want to learn more about logic gates, you can read the webpages in the references below.
References and Credits
- (n.d.). Logic Gates – Tutorialspoint. Retrieved November 28, 2021, from https://www.tutorialspoint.com/computer_logical_organization/logic_gates.htm
- Sam Sattel. (n.d.). How Logic Gates Work in Digital Electronics. Retrieved November 28, 2021, from https://www.autodesk.com/products/eagle/blog/you-shall-not-pass-how-logic-gates-work-in-digital-electronics/
- Emmanuel Ikimi. (n.d.). What Are Logic Gates and Why Are They Important? Retrieved November 28, 2021, from https://www.electronicspoint.com/research/what-are-logic-gates-and-why-are-they-important/
- In One Lesson. (2011, October 12). 💻 – See How Computers Add Numbers In One Lesson. Retrieved November 28, 2021, from https://www.youtube.com/watch?v=VBDoT8o4q00